Setting up a YSO model

Setting up a YSO model#

Note

If you haven’t already done so, please make sure you read the Important Notes to understand whether to specify dust or dust+gas densities!

Source parameters#

The stellar luminosity and radius should be set via the following attributes:

m.star.luminosity = 5 * lsun
m.star.radius = 2 * rsun

and either the temperature or the spectrum of the source can be set, using:

m.star.temperature = 10000.

or:

m.star.spectrum = (nu, fnu)

Flared disks#

Flared disks can be added using the add_flared_disk() method, and capturing the reference to the FlaredDisk object to set the parameters further:

disk = m.add_flared_disk()
disk.mass = 0.01 * msun             # Disk mass
disk.rmin = 10 * rsun               # Inner radius
disk.rmax = 300 * au                # Outer radius
disk.r_0 = 100. * au                # Radius at which h_0 is defined
disk.h_0 = 5 * au                   # Disk scaleheight at r_0
disk.p = -1                         # Radial surface density exponent
disk.beta = 1.25                    # Disk flaring power

Envelopes#

Power-law spherically symmetric envelope#

The simplest kind of envelope is a spherically symmetric envelope with a power-law distribution in density. A power-law envelope can be added using the add_power_law_envelope() method, and capturing the reference to the PowerLawEnvelope object to set the parameters further:

envelope = m.add_power_law_envelope()
envelope.mass = 0.1 * msun          # Envelope mass
envelope.rmin = au                  # Inner radius
envelope.rmax = 10000 * au          # Outer radius
envelope.power = -2                 # Radial power

Ulrich rotationally flattened envelope#

A more complex envelope density distribution is that of Ulrich (1976), which consists of a rotationally flattened envelope. A power-law envelope can be added using the add_ulrich_envelope() method, and capturing the reference to the UlrichEnvelope object to set the parameters further:

envelope = m.add_ulrich_envelope()
envelope.mdot = 1e-4 * msun / yr    # Infall rate
envelope.rmin = 0.1 * au            # Inner radius
envelope.rc = 100 * au              # Centrifugal radius
envelope.rmax = 1000 * au           # Outer radius

As mentioned in the Important Notes, the infall rate mdot is not necessarily the dust+gas infall rate - for instance if the dust opacities are per unit dust mass, the infall rate specified should only include the dust (because it is only used to set the density structure, and does not add any accretion luminosity).

Note

the Ulrich (1976) solution is sometimes (incorrectly) referred to as the Terebey, Shu, and Cassen (TSC) solution, which is much more complex. The Ulrich envelope implemented here is the same envelope type as is often implemented in other radiation transfer codes.

Bipolar cavities#

Once an envelope has been created, bipolar cavities can be carved out in it by calling the add_bipolar_cavities method on the envelope object, which returns a BipolarCavity instance:

cavity = envelope.add_bipolar_cavities()
cavity.power = 1.5                  # Shape exponent z~w^exp
cavity.r_0 = 1.e-20                 # Radius to specify rho_0 and theta_0
cavity.theta_0 = 10                 # Opening angle at r_0 (degrees)
cavity.rho_0 = 1.e-20               # Density at r_0 in g/cm^3
cavity.rho_exp = 0.                 # Vertical density exponent

Ambient medium#

In addition to disks and envelopes, it is also possible to add a constant ambient density medium using the add_ambient_medium() method, which returns an AmbientMedium instance:

ambient = m.add_ambient_medium()
ambient.rmin = 0.1 * au            # Inner radius
ambient.rmax = 1000 * au           # Outer radius
ambient.rho = 1.e-20               # Ambient density in g/cm^3

By default, the ambient medium simply adds a constant density to any pre-existing density. However, in some cases you may want to use this as a minimum density. In order to do this, set the subtract attribute to a list containing any component you want to subtract from the constant density:

disk = m.add_flared_disk()
...
envelope = m.add_ulrich_envelope()
...
ambient = m.add_ambient_medium()
...
ambient.subtract = [envelope, disk]

In regions where the sum of the densities from these components exceeds the ambient density, no dust is added to the model, whereas in regions where the sum of the density of the components is below the ambient density, the density gets set to the ambient density.

Accretion#

Viscous dissipation#

Note

This feature is still experimental, please use with caution and report any issues!

To simulate the effects of accretion due to viscous dissipation of energy in the disk, you can use an ‘alpha accretion’ disk instead of a plain flared disk. Such disks can be added using the add_alpha_disk() method, and capturing the reference to the AlphaDisk object to set the parameters further. The parameters are the same as for flared disks:

disk = m.add_alpha_disk()
disk.mass = 0.01 * msun             # Disk mass
disk.rmin = 10 * rsun               # Inner radius
disk.rmax = 300 * au                # Outer radius
disk.r_0 = 100. * au                # Radius at which h_0 is defined
disk.h_0 = 5 * au                   # Disk scaleheight at r_0
disk.p = -1                         # Radial surface density exponent
disk.beta = 1.25                    # Disk flaring power

except that the accretion properties of the disk can also be specified. Either the disk accretion rate can be specified:

disk.mdot = 1e-6 * msun / yr        # Disk accretion rate

or the accretion luminosity from viscous dissipation:

disk.lvisc = 0.01 * lsun

As mentioned in the Important Notes, the disk accretion rate mdot should always be the total dust+gas accretion rate, because it is the total dust+gas accretion rate that sets the accretion luminosity.

Note that this accretion luminosity only includes the luminosity down to disk.rmin, and does not include the luminosity from the stellar surface (see Magnetospheric accretion). For more details on the accretion luminosity from viscous dissipation, see AlphaDisk.

Magnetospheric accretion#

Note

This feature is still experimental, please use with caution and report any issues!

Another important component of the accretion luminosity is that from the dissipation of energy as matter accretes onto the central star from the inner edge of the gas disk. In a simplistic model of magnetospheric accretion, matter free-falls from the radius at which the disk is truncated by the magnetosphere to the surface of the star. Half the energy goes into X-rays, and half goes into heating spots on the stellar surface, and is then re-emitted with a spectrum hotter than the rest of the stellar surface.

To help set this up, a convenience method setup_magnetospheric_accretion() is provided, which takes the accretion rate, the radius at which the matter free-falls from, the spot covering fraction, and optionally parameters describing the X-ray spectrum. For example:

m.setup_magnetospheric_accretion(1.e-6 * msun / yr, 5 * m.star.radius, 0.2)

will set up an X-ray and a hot spot emission component from the central source. The method does not currently set up actual spots, it assumes that the spots cover the star uniformly, and the spot covering fraction determines the temperature of the hot spots (a smaller covering fraction results in a larger hot spot temperature for a fixed accretion rate).

See setup_magnetospheric_accretion() for more details.

Dust#

The dust file to use for each component should be specified using the dust attribute for the component, e.g.:

disk.dust = 'www003.hdf5'
envelope.dust = 'kmh.hdf5'
cavity.dust = 'kmh_hdf5'

The dust can be specified either as a filename or an instance of one of the dust types.

Grid#

The gridding of the density can done automatically, but you will need to specify a grid size. Either a spherical polar or cylindrical polar grid can be used. To use the spherical polar grid:

m.set_spherical_polar_grid_auto(n_r, n_theta, n_phi)

and to use the cylindrical polar grid:

m.set_cylindrical_polar_grid_auto(n_w, n_z, n_phi)

The grid is set up in such a way as to provide very fine resolution at the inner edge of the disk or envelope, and logarithmic spacing of cell walls on large scales.

In some cases, this automated gridding may not be appropriate, and you may want to specify the grid geometry yourself, for example if you have other sources of emission than the one in the center. In this case, the set_spherical_polar_grid() and set_cylindrical_polar_grid() methods described in Coordinate grids and physical quantities can be used. As a reminder, these take the position of the walls as arguments rather than the number of cells, e.g.:

r = np.logspace(np.log10(rsun), np.log10(100 * au), 400)
r = np.hstack([0., r])  # add cell wall at r=0
theta = np.linspace(0., pi, 201)
phi = np.array([0., 2 * pi])
m.set_spherical_polar_grid(r, theta, phi)

Optically thin temperature radius#

When setting up the disk or envelope inner/outer radii, it can sometimes be useful to set it to a ‘dynamic’ quantity such as the sublimation radius of dust. A convenience class is available for this purpose:

from hyperion.util.convenience import OptThinRadius

The OptThinRadius class allows you to simply specify a temperature T_d, and when preparing the model, the code will pick the radius at which the temperature would be equal to the value specified if the dust was optically thin:

r = r_{\star}\,\left\{1-\left[1-2\,\frac{T_d^4}{T_{{\rm eff}}^4}\frac{\kappa_{\rm plank}(T_d)}{\kappa_{\star}}\right]^2\right\} ^ {-1/2}

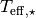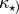where T_{{\rm eff,}\star} is the effective temperature of the central source, and \kappa_{\star)} is the mean opacity to a radiation field with the spectrum of the central source. In practice, you can use this as follows:

disk = m.add_flared_disk()
disk.mass = 0.01 * msun
disk.rmin = OptThinRadius(1600.)
disk.rmax = 300. * au
...

and the inner disk radius will be set to the radius at which the optically thin temperature would have fallen to 1600K, emulating dust sublimation.

Contents