Forced interactions¶
Hyperion includes several algorithms for forcing first interactions during the
photon propagation when making images. In classical Monte-Carlo propagation, the
pathlength for photon packets to travel is sampled from 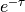 .
However, this can be inefficient in the following situations:
.
However, this can be inefficient in the following situations:
- If the optical depths in the model are very low, photons may escape the grid without ever interacting with the dust. This is an issue when computing images with the peeling-off method, since this method relies on interactions of the photon packets with the dust. For very optically thin models, unrealistically large numbers of photons may therefore be needed to get an acceptable signal-to-noise in the images.
- If some of the dust in the model is shielded from sources of emission by material with very high optical depths, those regions may end up never seeing any photons directly from the source. Indeed, only two in a billion photons will propagate through an optical depth of just 20. However, low probability direct photons from the source may in some cases be the dominant source of heating at high optical depths.
To mitigate these effects, various algorithms have been designed to modify the sampling of the pathlengths to travel. These algorithms implemented in Hyperion are described in detail below. In both cases, the energy of the photon packets are adjusted during the forcing to make sure that energy is conserved.
Note
These algorithms only affect the iteration of the radiative transfer during which the images are generated, not the initial iterations during which the temperatures are computed.
Wood and Reynolds (1999)¶
This algorithm is well suited to
situations where the optical depth in the model is low. The main idea of the
algorithm is to replace the sampling of 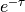 by sampling of a probability
density function that follows
by sampling of a probability
density function that follows 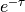 but is truncated and goes to zero
for
but is truncated and goes to zero
for  , where
, where 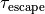 is the optical depth
for the photon to escape the grid. This then guarantees that an interaction
will occur before the photon escapes the grid.
is the optical depth
for the photon to escape the grid. This then guarantees that an interaction
will occur before the photon escapes the grid.
Baes et al. (2016)¶
This algorithm was developed to avoid the
issue with high optical depth described above. This algorithm replaces the
sampling of 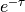 by sampling of a probability density function that
is a linear combintion of a truncated exponential (as in Wood and Reynolds 1999)
and a constant out to the edge of the grid. This ensures that even when using
realistic number of photons, interactions will occur at high optical depths.
The relative fraction of the constant is set by a parameter
by sampling of a probability density function that
is a linear combintion of a truncated exponential (as in Wood and Reynolds 1999)
and a constant out to the edge of the grid. This ensures that even when using
realistic number of photons, interactions will occur at high optical depths.
The relative fraction of the constant is set by a parameter 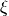 . When
. When 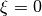 ,
the sampling is the same as in the Wood and Reynolds (1999) algorithm, and when
,
the sampling is the same as in the Wood and Reynolds (1999) algorithm, and when
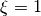 , the optical depth to the next interaction is sampled linearly between
, the optical depth to the next interaction is sampled linearly between
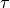 and
and 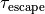 .
.
Setting the algorithm to use¶
By default, the Wood and Reynolds (1999) algorithm is used (but note that this may change in future). To turn off any forced interactions, once a model has been defined, you can do:
m.set_forced_first_interaction(False)
To explicitly set the algorithm to Wood and Reynolds (1999) (to guard against future changes in the default), you can do:
m.set_forced_first_interaction(True, algorithm='wr99')
Finally, to explicitly set the algorithm to Baes et al. (2016), you can do:
m.set_forced_first_interaction(True, algorithm='baes16', baes16_xi=0.3)
where baes16_xi is the 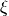 parameter described above.
parameter described above.